XAFSmass
XAFSmass A program for calculating the mass of XAFS samples April 2012 |
| pay also your attention to my programs for EXAFS and XANES |
| The 32-bit version is finally out. Now it can be natively run under 64-bit Windows. Many thanks to Roman Chernikov (Hasylab-DESY) for making it available! |
- Author: Konstantin Klementiev
- Theoretical references used:
- http://www-cxro.lbl.gov/optical_constants/
B.L. Henke, E.M. Gullikson, and J.C. Davis, X-ray interactions: photoabsorption, scattering, transmission, and reflection at E=50-30000 eV, Z=1-92, Atomic Data and Nuclear Data Tables Vol.54 (no.2), 181-342 (July 1993) - http://www-phys.llnl.gov/Research/scattering/index.html
Lynn Kissel, B. Zhou, S. C. Roy, S. K. Sen Gupta and R. H. Pratt, Validity of Form-Factor, Modified-Form-Factor and Anomalous-Scattering-Factor Approximations in Elastic Scattering Calculations Acta Crystallographica A51, 271-288 (1995).
R. H. Pratt, Lynn Kissel and P. M. Bergstrom, Jr., New Relativistic S-Matrix Results for Scattering - Beyond the Usual Anomalous Factors/ Beyond Impulse Approximation, in Resonant Anomalous X-Ray Scattering, edited by G. Materlik, C. J. Sparks and K. Fischer (North-Holland: Amsterdam, 1994).
P. P. Kane, Lynn Kissel, R. H. Pratt and S. C. Roy, Elastic Scattering of Gamma-Rays and X-Rays by Atoms, Physics Reports 140, 75-159 (1986).
Lynn Kissel and R. H. Pratt, Rayleigh Scattering - Elastic Photon Scattering by Bound Electrons, in Atomic Inner-Shell Physics, edited by Bernd Crasemann (Plenum Publishing: New York, 1985). - http://www.bmsc.washington.edu/scatter/periodic-table.html
ftp://ftpa.aps.anl.gov/pub/cross-section_codes/
S. Brennan and P.L. Cowan, A suite of programs for calculating x-ray absorption, reflection and diffraction performance for a variety of materials at arbitrary wavelengths Rev. Sci. Instrum. 63, 850-853 (1992) - http://physics.nist.gov/PhysRefData/FFast/Text/cover.html
http://physics.nist.gov/PhysRefData/FFast/html/form.html
C. T. Chantler, Theoretical Form Factor, Attenuation, and Scattering Tabulation for Z = 1 - 92 from E = 1 - 10 eV to E = 0.4 - 1.0 MeV J. Phys. Chem. Ref. Data 24, 71-643 (1995) - http://physics.nist.gov/PhysRefData/Xcom/Text/XCOM.html
J.H. Hubbell, Photon Cross Sections, Attenuation Coefficients and Energy Absorption Coefficients from 10 keV to 100 GeV, Natl. Stand. Ref. Data Ser. 29 (1969). J.H. Hubbell, Photon Mass Attenuation and Mass Energy-Absorption Coefficients for H,C,N,O,Ar and Seven Mixtures from 0.1 keV to 20 MeV, Radiat. Res. 70, 58-81 (1977). - http://ixs.csrri.iit.edu/database/programs/mcmaster.html
http://cars9.uchicago.edu/~newville/mcbook/
W. H. McMaster, N. Kerr Del Grande, J. H. Mallett, and J. H. Hubbell Compilation of X-Ray Cross Sections Lawrence Livermore National Laboratory Report UCRL-50174 Section II Revision I (1969) available from National Technical Information Services L-3, U.S. Dept. of Commerce - Usage:
- Calculation of mass and absorption step for powder samples
- Calculation of thickness and absorption step for samples with known density
- Calculation of gas pressure for ionization chambers
- Calculation of an unknown elemental concentration
- Calculation of two unknown elemental concentrations
- Finding the scattering factors f''
- Citation: You are requested to cite XAFSmass as: "K. V. Klementiev, XAFSmass, freeware: www.cells.es/Beamlines/CLAESS/software/xafsmass.html"
| Notice that you typically do not need the calculated values at exactly the edge position but rather at an energy somewhere above it. The list of edges does not force you to use those exact energies. I suggest you to edit the energy field manually. |
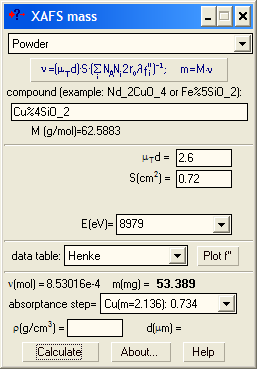
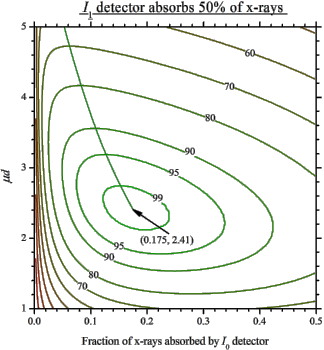
A typical application is the calculation of the mass for a powder sample. The optimal optical sample thickness μd depends on the absorption levels selected for the ionization chambers (see below). Typically, μd is between 2 and 3 (e.g. for a 17.5% absorption level for the 1st chamber and a 50% level for the 2nd chamber, the optimal thickness is 2.41). However, if you get the absorption step more that 1.5, it is recommended to reduce the sample mass to avoid potential thickness effect due to possible inhomogeneity in the wafer. If your sample is diluted and you get a very low absorption step, do not try to make the wafer thicker hoping that you will get better spectra - you will not: The optimal thickness gets the best signal-to-noise ratio (it is in this sense it is optimal). You can only try to measure your absorption spectra with another registration technique: in fluorescence or electron yield modes.
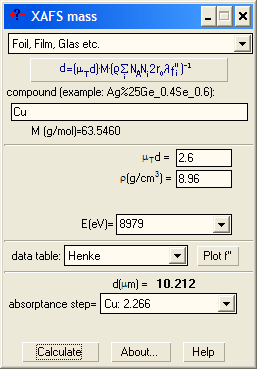
Here you can calculate the thickness of the sample with known density (usually, a foil). Commercial foils are highly homogeneous in thickness, so that you may ignore large step jumps and pay attention to the total μd only.
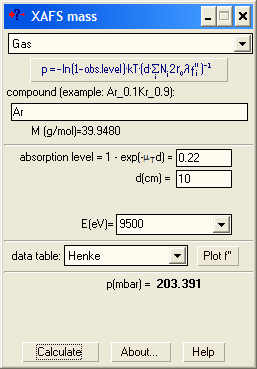
For nitrogen, do not forget the 2: N_2, not just N.
Start with the 2nd ionization chamber (IC). If a reference foil is placed between the 2nd and the 3rd IC, the fraction of x-rays absorbed by the 2nd IC is usually set to 50%. If the reference foil is not needed, one can select total absorption (100%). For these two cases the optimal absorption of the 1st IC at a certain μd is found from the following figures showing the levels of signal-to-noise ratio:
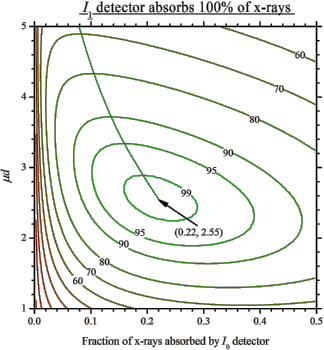
Case 1: You know the composition of the matrix.
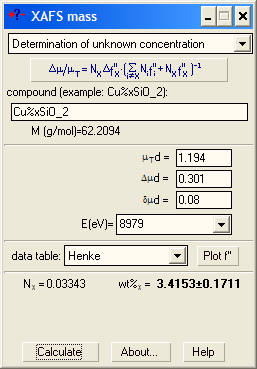
You need an absorption spectrum taken without the sample (empty spectrum) but with the same state of the ionization chambers. You then subtract it from the spectrum of the sample (e.g. in VIPER) and get a real (i.e. not shifted vertically) absorption coefficient. Determine the value of μd above the edge (μTd), the edge jump (Δμd) and its uncertainty (δμd). Specify the chemical formula with x.
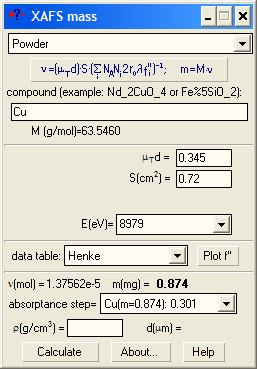
Case 2: You know the sample mass and area.
Determine the edge jump (Δμd). For the pure element find such a value for μTd that the absorption step in the pull-down list was equal to your experimental Δμd. This will give you the mass of the element of interest. Just divide it by the total mass to get the weight percentage.
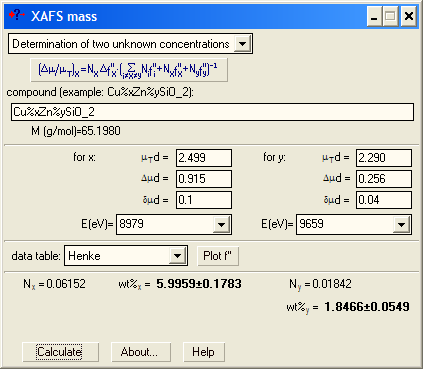
Here you also need empty spectra (for each of the two edges) to find the unshifted values for absorption coefficient above both edges.
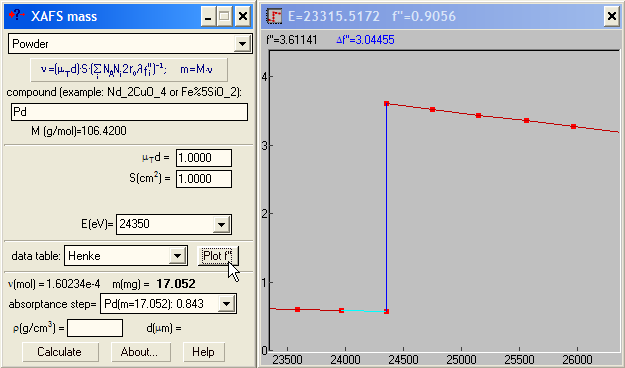
If you need to know the scattering factor f'' at different energies and/or its jump at an edge (Δf''), XAFSmass provides a graphical tool for this.
For example, you may need these values to determine the composition of a binary compound if you have the experimental edge heights at two edges.
The absorption step Δμd at the absorption edge of energy E is proportional to Δf''ν/E, where ν is the amount of (resonantly) absorbing atoms in mole. Hence, the atomic ratio of two elements in the same sample is νA/νB = (Δμd)A/(Δμd)B ·[Δf''A/Δf''B · EA/EB]. For binary compounds AxB1-x the concentration x is calculated then as x = (νA/νB)/[1+(νA/νB )].
| pay also your attention to my programs for EXAFS and XANES |